In the May 2009 edition of Miller-McCune magazine, and then later on Miller-McCune.com, we printed a letter from Wharton’s Howard Wainer that challenged some statistics from a story on wrongful convictions by Steven Weinberg. However, the statistics presented by professor Wainer — or perhaps it was the assumptions he made — seemed intuitively, ummm, suspect. (See the original exchange below.) So we opened up the floor for our readers to tell us what they thought.
As our Editor John Mecklin challenged at the time: “We still suspect that professor Wainer knows his statistics cold but scored less well in Assumption Making 101. If you know we’re right or wrong, … tell us why. Our comments section awaits your brilliance.”
And you did. Herewith is a sample of the responses:
Epidemiology Lacking
With all due respect, in response to professor Wainer, who is a likely expert in econometrics but perhaps not in epidemiology, let me first present a few basic epidemiological equations that are often used when examining the effectiveness of medical tests and/or screenings in public health. With the exception of the first two listed measures, each of these metrics addresses a different type of question with regard to the effectiveness of a given medical test or screening procedure. The first metric is listed because it will be needed later. The second and final four metrics are listed for thoroughness, although they will not be used herein.
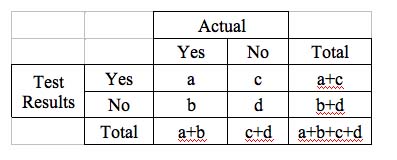
Prevalence: (a + b) / (a + b + c + d)
Incidence: the proportion of a population with disease developing during a specified time period.
Sensitivity: a / (a + b)
Specificity: d / (c + d)
Positive Predictive Validity: a / (a + c)
Negative Predictive Validity: d / (b + d)
Percentage in Agreement (a + d) / (a + b + c + d)
Percentage in Disagreement (b + c) / (a + b + c + d)
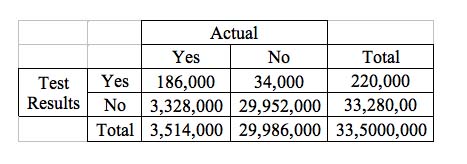
Using the professor’s data and statistics for breast cancer and constructing the appropriate 2-by-2 table, we find:
As you might recall and can certainly check to see, the professor’s statement and equation related to breast cancer were as follows:
Thus, if you have a mammogram and it results in a positive (you have cancer) result, the probability that you have cancer is:
186,000/(186,000+3.35 million) = 4 percent
The professor’s equation is in the general form of “a / (a + ‘approximately’ b).” This value approximates the sensitivity of the screening, defined as: the probability of a positive test among patients with disease. So, his interpretation is functionally backwards and disregards both the physical inception and the developmental staging of the disease. At approximately 4 percent for the screening’s sensitivity, it is easy to understand why periodic screening is important. As the mainly too small to be detected cancers grow over time, future screening would hopefully find the developing cancers in time for an effective treatment. Quite the opposite of his interpretation, professor Wainer’s statistics mean that a positive result (potential cancer) should be taken very seriously, and a negative result should be interpreted as there is nothing large enough or suspicious enough to call the test positive, for now. It does not mean cancer-free. It means that cancers could be present but are too small or innocuous looking to trip a positive test result.
For the actual statistic that professor Wainer seeks to answer his question (i.e., the probability of disease given a positive or negative test), Reverend Bayes was the first to address the issue in the late 1800s when he developed an equation to relate the probability of disease before ordering the test (the pre-test probability) to the probability of disease given a positive or negative test (the post-test probability). The Bayes equation to address professor Wainer’s equation is shown below:
Which equals 0.006 / 0.007 and rounds to the 85 percent probability stated by professor Wainer for the odds of having breast cancer if given a positive test result (“Mammograms identify breast cancers correctly 85 percent of the time”). The numbers should match, insofar as the equation addresses the actual question asked by professor Wainer, rather than the one he answered with his equation. Alternatively, professor Wainer’s work points to the fact that we lack a test that will reliably detect breast cancers when they are only a few cells in number and not large enough in size or suspicious enough in appearance to be recognizable as cancerous cells until they have further developed.

The real problem is not that professor Wainer uses the wrong formula to answer his question. The problem is that a potentially large number of women might read his writings, believe him, and then not seek timely follow-up attention after receiving a positive mammography screening result, due to now believing that their odds of actually having cancer would be about 4 percent. It is one thing to be wrong, but it is quite another to be wrong in a way that could shape policy or personal actions such that a substantial portion of an entire population could be placed at an added and unnecessary risk.
If my analysis is incorrect and professor Wainer is actually correct, I await being shown where and how.
Dana Keller, Ph.D.
President, Halcyon Research, Inc.
Author of: The Tao of Statistics and The Tao of Research
Nice Shot, Wrong Target
I believe Professor Wainer’s statistics are first rate. Sadly, I think he aimed his considerable analytical skills at the wrong target. And, like you, I think his assumptions were, well, assumptive.
Or, as my father the cop used to say, “That was a perfect shot. Sadly, it was aimed at the wrong target.” Let us see if we can find a target more amenable to the good professor’s efforts.
While it may be interesting to look at this in terms of, uh, “macro society,” the first problem is that using the figure of 300 million, or even six of one and one-half dozen of the other, assumes that all 300 million are innocent. I don’t believe that for a second, and neither do you. Why, a goodly number of our neighbors are probably out there right now, performing nefarious deeds under our very noses. So let’s dispense with the idea of counting noses all over American society, whether they’re good noses or bad.
No, in this example what is wanted is the number of persons waylaid by the criminal justice system. It’s a question of how many of our brethren and sistren (I totally made that word up, by the way), are doin’ time. Knowing that figure, we can then deduce what fraction of them is probably innocent. Not that I believe it for a second, I’m just saying.
The most recent figure I saw put the total number of incarcerated persons in the United States at 3.5 million, which seems high, but, for the moment, let’s go with it. Feel free to substitute your own data. The Professor invites us to assume that the criminal justice system, or at least the valid prosecution of our fellow citizens, is probably close to 99.9 percent accurate. I’m fine with that. It makes me giggle, but I’m fine with it.
So, let’s just plug that formula into our reverse polish notated handheld calculating device and answering machine and … (if you have a drum roll handy, now’s the time) … hey presto, .01 percent of 3.5 million miserable souls comes out to about 35,000 even more miserable souls because they might be innocent.
That’s the number we should be talking about, not all of our fellow hoodlums who are still out on the street, worrying old women, reading the funny papers without paying for the whole paper, asking for soy lattes, stuff like that.
The reason it doesn’t work, for those of you who haven’t quite caught up, is that the whole 300 million of us are NOT under investigation, didn’t get arrested, didn’t get arraigned and were not prosecuted. The ones who DID go through that whole dance are the only ones that matter in the current analysis.
Now, 35,000 actually innocent but prosecuted and stuffed in some kind of pokey anyway people is still way too high a number, especially if you personally are one of the 35,000, but, in a free and sort of democratic society, it’s still pretty good.
The real question is, what are we going to do with the actually innocent rotting away in jail? I mean, does it really matter what the actual percentage, or the raw number, ends up being, if, at the end of the day, we end up with a number that represents actual people wrongly convicted and serving time. Clearly, I can’t answer that, but I do hope that very smart people with very smart ideas will, at some point, try to find a solution that doesn’t start, or end, with possibly guilty people going free. But that’s a whole ‘nother math quiz. Or two.
Of course, having said all of the above, I am now highly suspicious of all y’all, and will be watching you closely.
James E. Mason
Las Vegas, Nev.
And Now for an Instant Mea Culpa …
You know that thing that happens when you’re trying to show how smart you are, especially at someone else’s expense, and instead you end up demonstrating that you’re a gigantic jackass that doesn’t know how to count after all? I fear that happened to me. I’m blaming my computer, and I’m sticking to it, because the computer is not in a position to defend itself, but, at the end of the day, my calculation was dead-ass wrong.
The plain fact is that .01 PERCENT of 3.5 million incarcerated souls is, wait for it, only 350, a figure I deduced all by myself when I realized I had actually calculated 3.5 million times point oh one (.01), not 3.5 million times .01 percent, which is an entirely different, if smellier, kettle of fish.
I know, I suck. Don’t get me wrong, 350 people is barely enough to get a working crime syndicate together, but it’s still a lot of people if you’re one of the people, which is sort of the point.
Nevertheless, the number is a whole lot less than it ought to be if there’s a major problem with incarcerating innocent people. On balance, then, our now totally and amazingly correct calculation shows that, while there may be a problem, what with potentially 350 innocent people hanging around in leg irons and eating bad food, it’s still only a drop in the bucket, cosmically, and certainly not enough to justify upending our justice system over.
As for me, I’ll sleep WAY better tonight knowing that Mrs. Faducci’s mathematical ministrations were not totally wasted on me, and I’ll be delighting in the fact that it only took me, what, four hours or so, to see the error of my ways. That has to be some kind of record, for me anyway.
James E. Mason
Las Vegas, Nev.
Picking Numbers Out of Air …
We have no way of judging the accuracy of professor Wainer’s assumption “that the criminal justice system is 99.9 percent accurate” without knowing how many people are in prison or are sent to prison each year. His example would have been easier to comprehend if he had started with the number of people convicted of a crime each year and an assumption of judicial system accuracy. As used by professor Wainer, judicial system accuracy could be 99.99 percent or even 99.999 percent (1 out of every 100,000 people living in the U.S. wrongly convicted).
Here is another way of estimating the probability that a person found guilty of a crime is in fact guilty.
To be found guilty you must first be charged and then tried in court. None of the other 300 million people in the country matter.
Assume that the probability of the truly guilty person being charged and tried is 3/4 (75 percent). Also, assume that the probability of this person being convicted is 2/3 (67 percent). Therefore the probability of an innocent person being charged and tried is 1/4 (25%). Assume that the probability of this person being convicted is 1/5 (20%). Then, for every 100 people charged and tried, 75 will be guilty, of which 50 (75 x 2/3) will be found guilty. The remaining 25 people charged and tried will be innocent, of which 5 (25 x 1/5) will be found guilty. Therefore, 50 guilty people will be found guilty and five innocent people will be found guilty. The probability that a person found guilty is in fact 50/(50+5) or 50/55, which is 91 percent!
This is clearly a much different outcome than that presented by Professor Wainer and also clearly shows that the whole exercise is totally dependent upon the assumptions. Also, the math is much closer to fourth-grade arithmetic than it is to “Statistics.”
Tim Schilling
St. Augustine, Fla.
There’s a LOT of Criminality Out There
Editor, your Editorial Challenge regarding Dr. Wainer’s statistical conclusion — that the probability of being guilty given that one is truly guilty is 3 percent — is right on the mark. Wainer’s counterintuitive finding is a mathematically correct application of Bayes’ Theorem (if one reads a bit into his assumptions). However, your speculation that the problem is with Dr. Wainer’s assumptions is correct. A quick check of crime statistics in the U.S. shows that there were 11 million crimes committed in 2007; Wainer assumed 10,000 — over 1,000 times smaller than the actual number of crimes. If one replaces the number 10,000 in Wainer’s calculations with 11,000,000, the probability that a person who is found guilty is truly guilty is 97 percent in contrast to his figure of 3 percent. I imagine that I am not the only person who noted this unrealistic assumption made by my friend Howard Wainer.
Alan Nicewander
Monterey, Calif.
Population Implosion
I’m no professor, but I do find flaw with Wainer’s argument. I think the issue is what the ‘population’ is in statistical terms —and it’s not the physical population of the United States, but rather the number of events to which the analysis applies. In this case, the ‘population’ statistically speaking should be the number of crimes handled by the authorities.
To illustrate the flaw with a counter-example, imagine that a magical comet passed overhead and every ‘good’ person (one who commits no crime) got cloned into two ‘good’ people overnight, but all the bad people were unaffected. To use Wainer’s illustrative numbers, we would then still have 10,000 ‘bad’ people committing crimes, but now 599,990,000 people overall. Unless the ‘bad’ people suddenly doubled their efforts, the number of crimes committed would still be the same, spread over a larger number of victims. By Wainer’s logic, an additional 299,990 would nonetheless be incarcerated in short order, even though the number of crimes committed and handled by the authorities was unchanged.
Jeff Sandgren
Sewell, N.J.
Positive About the Negative
There are at least two problems apparent in Wainer’s example. First, the justice system is to assign responsibility for specific crimes. If there are 10,000 crimes, and the system gets it right 99.9 percent of the time and identifies 9,990 individuals who have committed crimes, as described in the example, there are only 10 crimes left.
Second, the overall correct rate of 99.9 percent is in fact not polyannish. In a country of 300,000,000, if there are 10,000 crimes, I could make a correct decision about whether any individual committed the crime 99.997 percent of the time without any information simply by declaring everyone innocent. I would make 290,000,000 correct choices and 10,000 incorrect ones. My rate would go up fairly dramatically for any piece of information that definitively ruled out large segments of the population as being incapable of committing the crime. I could for example rule out very young children, individuals in nursing homes, individuals already in prison and my correct rate would go up.
The confusion would seem to be between overall correct rate versus the predictive value of a positive screen and the predictive value of a negative screen. When we talk about error rates in criminal justice, we are uniformly talking about the predictive value of a positive (guilty) adjudication. If our justice system is correct in assigning guilt 99 perent of the time, then 1 percent of those found guilty would be innocent. The predictive value of a negative (not identified, investigated, charged, convicted) is much higher than that, at least for the commission of any specified crime.
Kenneth Leonard, Ph.D.
Research Institute on Addictions
and Department of Psychiatry
University at Buffalo
Simple Illustration of the Complex
Professor Wainer is entitled to hypothesize an “accuracy rate” of 99.9 percent for criminal justice. He is also allowed to hypothesize a group of 10,000 structured in a most unusual way. If he defines accuracy rate as the percent of convicted who are truly guilty, he can then determine the number of correct and incorrect convictions among his 10,000 under his scenario. What he is not entititled to do is apply his hypothetical error rate of .001 to his ‘innocent’ population of 300 million. The reasons are complex but we can use an example — as does Wainer.
Hypothesize an accuracy rate of 100 percent — surely a trivial difference from 99.9 percent. Now his ratio becomes 10,000/10,000 + .00 (300 million) which = 1.00 and the probability of an innocent having been convicted is zero, not his 97 percent. This is so regardless of the number of true criminals. It is also as legitimate a conclusion as Wainer’s and illustrates the dangers of such statistical speculation.
Norm Wallen
Flagstaff, Ariz.
And now for the original letter: (Go back to top.)
For Those of You Who Paid Attention in Statistics Class…
Can we ever prevent the imprisonment of innocent people?
Following up on Steve Weinberg’s article (“Innocent Until Reported Guilty,” October 2008) and the subsequent commentary, let me offer a sad but sober dose of mathematical reality. The conclusion is that so long as only a very small minority of people commit crimes and the criminal justice system is fair (“fair” meaning that all people are equally subject to investigation) there will always be a very large proportion of innocent people convicted.
Now the supporting argument, made by way of an example:
Suppose there are 10,000 true criminals in the United States annually. I don’t know how many there really are, but let’s assume 10,000 for the example.
Second, let’s assume that the criminal justice system is 99.9 percent accurate. By “system” I mean the entire system, starting with investigation and prosecution and ending with punishment. I know that 99.9 percent may be Pollyannaish, but, again, let’s accept it for the example. This means that the probability of a guilty person being caught and successfully tried, convicted and punished is 99.9 percent and the probability of an innocent person being convicted is but 0.1 percent.
Now let us ask and answer the key question: If a person is found guilty of a crime, what is the probability that s/he is guilty?
This probability is a ratio that has, in its numerator the number of guilty people successfully punished = .999 x 10,000 = 9,990. In the denominator is the number of guilty people being punished plus the number of innocent ones being punished. We already have the guilty part of this (9,990). The innocent part is .001 times the number of innocent people in the U.S., or .001 x 300,000,000 = 300,000.
So the answer to the question is:
9,990/(9,990+300,000) = 9,990/309,990 = 3%
Or, expressed another way, 97 percent of those in prison, under the circumstances of this example, would be innocent. Of course if the true number of criminals is 100,000, then the proportion of innocents is “only” 70 percent. It is amazing that so few horror stories are being told.
Howard Wainer
Professor of Statistics
The Wharton School
of the University of Pennsylvania
A question from the editor: We’d like to double-check some of your reasoning with you. You create a fraction with the number of people successfully punished in your example in the numerator (in this case, 9,990) and in the denominator, you use 300,000,000 as the number of innocent people in the U.S.
We were wondering, for your example to be valid, wouldn’t you have to place a number of “charged” innocent people in the denominator, and not the entire U.S. population?
A response from Wainer: Thank you for taking the time to read and think about my example. No, the denominator is as I have specified it. The figure 99.9 percent represents the probability of getting it right of the whole process — this means initial investigation, charging, prosecuting, convicting and imprisoning.
So it assumes that at the beginning of any investigation, everyone is under consideration (although a large proportion may be eliminated quickly). This assumption may not be true — it may be that some groups of people (the usual suspects) are always considered, and some never are. I was proceeding under the democratic assumption that initially at least we are all equal under the law.
Note, by the way, that the same arithmetic is informative in evaluating medical testing. Each year in the U.S., 186,000 women are diagnosed, correctly, with breast cancer. Mammograms identify breast cancers correctly 85 percent of the time. But 33.5 million women each year have a mammogram and when there is no cancer it only identifies such with 90 percent accuracy. Thus if you have a mammogram and it results in a positive (you have cancer) result, the probability that you have cancer is:
186,000/(186,000+3.35 million) = 4%
So if you have a mammogram and it says you are cancer free, believe it. If it says you have cancer, don’t believe it.
The only way to fix this matches your question — reduce the denominator. Women less than 50 (probably less than 60) without family history of cancer should not have mammograms.




