A physicist and mathematician sat down at lunch one day and discussed a complicated human problem: shared custody of children with ex-spouses.
By the end of that meal, they had transformed it into a “classical glass theory problem” and solved it.
The resulting study, published in The European Physical Journal B this month, offers a levelheaded, fair way of scheduling custody of children.
Lead author Andrés Gomberoff, a physicist at Universidad Andres Bello in Santiago, Chile, got the idea as he attempted to schedule his weekends. He juggles custody with his two ex-wives (he has children with both) and his current partner, who also has children by a previous relationship.
The children must spend every other weekend with each parent. He simply wanted to have all his children together on one weekend, and have time to spend alone with his current partner on the next.
During lunch with a few colleagues, including chaos-theory mathematician Pierre Paul Romagnoli, the group created a model to represent the problem.
The black circles represent single men, white circles are single women, and gray circles are current couples. Each line is a previous relationship that bore children, and the arrows indicate with which parent they are staying on a given weekend.
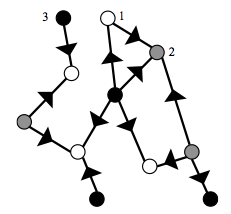
In this “custody arrangement state” (at right), the points represent the adults and the lines that connect two points represent their children. If each line has an arrow pointing to the parent with whom the children stay on a given weekend, Romagnoli says, “can you or can you not assign the arrows so that each vertex is all giving or all receiving?”
It’s unlikely that there’s a perfect solution, especially when, as in Gomberoff’s case, the network is large. But it’s possible when the number of connections is small.
The study also utilizes the spin-glass and maximum-cut problems to model the more complex issue of “maximizing happiness.” The researchers define a happy parent as one who has all their children on the same weekend.
The difficulty of this problem increases exponentially with each additional adult (or vertex). Romagnoli compared it to a Sudoku, where one additional line complicates the whole thing.
If your network has fewer than five people, then feel free to try this at home. “If you make a drawing on the board, you can solve it very fast. There’s not very many solutions,” Romagnoli says.
Of course, the researchers realize that real custody battles are more difficult to solve. “It’s a mathematical simplification,” Romagnoli says. Their study assumed all parties were heterosexual and willing to cooperate. It also assumes there’s no animosity between step-siblings.
The group may consider a follow-up study if they can get better demographic data on people with custody problems. If the findings are robust, judges can even use the models to help make decisions, Romagnoli says. “Divorces are messy, there are no straight rules, and usually the kids pay the price. If they want something that’s fairer, this model could help.”




